Pour évoquer le nombre d’or, vous devez d’abord abordé « La divine proportion. » Ce nombre est créatif, régénérateur et harmonieux, Il est parfois utiliser par des initiés comme signe de reconnaissance, mais aussi utiliser par certaines organisations qui détiennent ce savoir. `
Depuis la nuit des temps les plus reculés, artistes, sculpteur, musiciens, et peut-être même poètes ont fait de lui l’harmonique pivot de leurs œuvres. Un jour ou l’autre, Il a guidé mathématiciens, physiciens, botanistes, toutes les corporations d’investigateurs, scientifiques en somme, dans leurs explorations de la nature. Les égyptiens, les pythagoriciens ( Franc maçon ou initiés ), considéraient les nombres comme l’essence et le principe de toute chose, l’ingrédient fondamental de la naissance de l’univers. Les système qu’ils élaborèrent leur permit de toucher du doigt la relation entre humaine et divine nature, et les convainquit de l’existence, en effet, d’une sorte de code secret.
On appelait les disciples de Pythagore les mathématekoi, autrement dit « ceux qui étudient le tout.» L’Égypte antique avait été la première, la grande pyramide de Kheops est la plus importante de l’ensemble édifié a Giseh : Sa remarquable beauté tient à sa relation avec le nombre d’or. La nature disposerait-t-elle vraiment d’un code secret, accessible a la compréhension de l’esprit humaine ?
Sans laide d’outils aussi parfait… les initiés avait ce désir de décrire par les nombres l »harmonie sous-jacente d’un univers parfait. C’est ainsi qu’ils révélèrent le défi que leur lançait cette trouvaille inopinée, et jetèrent les bases d’une évolution possible des principes mathématiques.
La suite de Fibonacci est une suite d’entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent.
Elle commence généralement par les termes 0 et 1 (parfois 1 et 1) et ses premiers termes sont :
0, 1, 1, 2, 3, 5, 8, 13, 21, etc. (suite A000045 de l’OEIS)
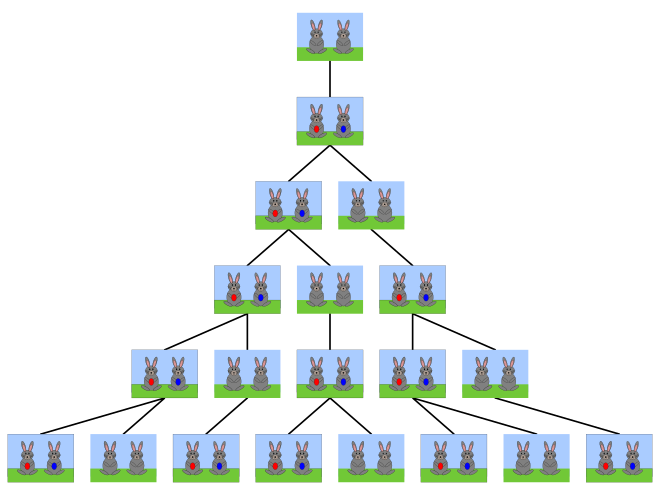
Elle doit son nom à Leonardo Fibonacci, dit Leonardo Pisano, un mathématicien italien du XIIIe siècle qui, dans un problème récréatif posé dans un de ses ouvrages, le Liber Abaci, décrit la croissance d’une population de lapins :
- « Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du troisième mois de son existence ? »
Cette suite est fortement liée au nombre d’or, φ (phi). Ce nombre intervient dans l’expression du terme général de la suite.
Inversement, la suite de Fibonacci intervient dans l’écriture des réduites de l’expression de φ (phi) en fraction continue :
Les quotients de deux termes consécutifs de la suite de Fibonacci sont les meilleures approximations du nombre d’or.
En géométrie, le nombre d’or est la valeur qui correspond au rapport entre deux longueurs a (la plus grande) et b (la plus petite) telles que (a+b)/a = a/b.
Le nombre d’or était déjà utilisé par les Grecs, comme par exemple dans le Parthénon (le temple que les Grecs consacraient à certains de leurs dieux) dont le fronton est inscrit dans un rectangle dont les longueurs des côtés adjacents ont le nombre d’or comme rapport. Les peintres et architectes comme Botticelli, Dali ou Le Corbusier, pour ne citer qu’eux, l’ont utilisé dans leurs oeuvres. Le nombre d’or est souvent associé à des qualités esthétiques particulières et à des proportions harmonieuses. On constate aussi généralement que le rapport de la taille d’une personne avec la hauteur de son nombril est proche du nombre d’or…
Dans la nature, on retrouve très souvent des motifs basé sur la suite Fibonacci et sur le nombre d’or. Il semblerait que la nature marque une prédilection pour la suite de Fibonacci et pour le nombre d’or.
- les animaux
- les fruits
- les Fleurs
- les marguerites
- les tournesols
- les cactus
- les monuments ( anciens comme récent )
- les étoiles de mer
- les coquilles de mollusques
- les pommes de pins (pives)
- les cyclones météorologiques
- les galaxies
- etc…
On remarque par exemple que le nombre de pétales des fleurs est souvent un des nombres de la suite de Fibonacci: 3, 5, 8, 13, 21, 34 ou 55. Par exemple, les lis ont 3 pétales, les boutons d’or en ont 5, les chicorées en ont 21, les marguerites ont souvent 34 ou 55 pétales, etc…
Dans certains objets de la nature, on observe aussi très souvent des spirales (spirales logarithmique) dans lesquelles intervient le nombre d’or. Cette spirale d’or s’inscrit dans un rectangle dont les proportions (rapport de la longueur sur la hauteur) correspondent au nombre d’or (on peut construire une spirale d’or en traçant des 1/4 de cercle dans chaque carré).
Pour expliquer pourquoi la nature semble si proche des mathématiques, il faut prendre en compte la question d’efficacité dans ces arrangements géométriques, par exemple pour favoriser le processus de croissance des plantes et l’optimisation du remplissage de l’espace. On peut se poser la question si l”esthétique géométrique n’aurait-elle pas le même effet sur les abeilles que les couleurs des fleurs, aidant ainsi à la pollénisation et donc à la reproduction des plantes? Cette fonction esthétique de la suite de Fibonacci n’a en réalité pas clairement été démontrée…
En finance dans l’analyse technique des marchés financiers, on utilise un outil appelé retracement de Fibonacci. Les retracements de Fibonacci correspondent généralement à des supports ou à des résistances naturelles sur lesquels les prix vont buter. On se base donc sur l’idée que l’on peut prédire les mouvements boursiers en fonction de ratios ou seuils qui font référence à la suite de Fibonacci. Les ratios sont obtenus en divisant un nombre de la suite de Fibonacci par le nombre suivant. Sachant que tous les analystes financiers et les traders de la planète regardent ces ratios, ils ont de fait un caractère auto-réalisateur.
Dans le morceau Lateralus du groupe américain de rock progressif Tool, le rythme et le nombre de syllabes des paroles suivent la suite de Fibonacci.
https://www.youtube.com/watch?v=wS7CZIJVxFY
-
Littérature :
-
- Da Vinci Code, de Dan Brown
- Maya Fox 2012, tome 1 : La prédestinée, de Silvia Brena et Iginio Straffi
- La Confrérie des Invisibles, de Kurt Aust (en)[réf. nécessaire]
- Le problème avec les lapins, d’Emily Gravett
- Les Pyramides de Napoléon, de William Dietrich
- Math Girls, d’Hiroshi Yuki
- Suite de Fibonacci et nombre d’or dans l’ensemble de Mandelbrot
- Suite de Fibonacci dans le dictionnaire des nombres
- Les suites de Fibonacci aléatoires, conférence de Benoît Rittaud à la Cité des sciences et de l’industrie
Partager ce savoir à vos proches en cliquant sur le bouton ci-dessous.
Paix et sincérité à tous.
Eveil-delaconscience






Vous devez vous connecter pour laisser un commentaire.