Des éléments qui se répètent, des bâtiments qui se ressemblent, des rues qui s’assemblent en un point névralgique… est-ce un hasard ou tout est fait pour être centré sur un seul point ( un fractale) ?
Je ne parlerais pas des monuments, des villes qui, elles aussi, sont construites de formes fractales. Connaissions-nous ces formes quand il a fallut construire des forts, il y a plus de 200ans ? C’est une question qui se pose selon mes recherches. Je vous laisse voir les propos fournis par wikipédia et vous fournis des vidéos en lien, qui pourront vous aider à approfondir les formes géométriques cachées de la vie.
Une figure fractale ou fractale (ou encore en anglais fractal), est une courbe ou surface de forme irrégulière ou morcelée qui se crée en suivant des règles déterministes ou stochastiques impliquant une homothétie interne.
Le terme « fractale » est un néologisme créé par Benoît Mandelbrot en 1974 à partir de la racine latine fractus qui signifie brisé, irrégulier (fractale n.f). Dans la « théorie de la
rugosité » développée par Mandelbrot, une fractale désigne des objets
dont la structure est invariante par changement d’échelle.
Ce terme était au départ un adjectif :
les objets fractals (selon un pluriel formé sur l’exemple de « chantiers navals »).
Les fractales sont définies de manière paradoxale, en référence aux structures gigognes
dont ils constituent des cas particuliers :
« Les objets fractals peuvent être envisagés comme des structures gigognes en tout point et pas seulement en un certain nombre de points, les attracteurs de la
structure gigogne classique.
Cette conception hologigogne (gigogne en tout point) des fractales implique cette définition tautologique : un objet fractal est un objet dont chaque élément est
aussi un objet fractal ».
Malgré les apparences, ce type de définitions de nature récursive
n’est pas seulement théorique mais peut concerner aussi des concepts
usuels :
un ancêtre est un parent ou un ancêtre d’un parent, un multiple
est un composé d’un nombre ou d’un multiple de ce nombre, un escalier
commence ou prolonge un escalier, une dynastie inaugure ou prolonge une
dynastie
Caractéristiques :
Un objet fractal possède au moins l’une des caractéristiques suivantes :
sa dimension de Hausdorff est strictement supérieure à sa dimension topologique.
Cette caractéristique est généralement prise comme définition même d’un
objet fractal.
Pour exprimer la chose autrement, un réseau d’irrigation est un déploiement de lignes (« en 1D ») qui offre des caractéristiques commençant à évoquer une surface (« en 2D »).
La surface du poumon (« en 2D ») est repliée en une sorte de volume (« en 3D »).
De façon imagée, les fractales se caractérisent par une sorte de
dimension non entière.
(Mandelbrot ne considère pas cette définition comme tout à fait satisfaisante.)
il a des détails similaires à des échelles arbitrairement petites ou grandes il est trop irrégulier pour être décrit efficacement en termes géométriques traditionnels ;
il est exactement ou statistiquement autosimilaire, c’est-à-dire que le tout est semblable à une de ses parties.
Les figures fractales n’ont pas à satisfaire toutes les propriétés
mentionnées ci-dessus pour servir de modèles. Il leur suffit de réaliser
des approximations convenables de ce qui intéresse dans un domaine de
validité donné.
(le livre fondateur de Mandelbrot Les Objets fractals en donne une grande variété d’exemples). La taille des alvéoles du poumon, par exemple, taille à partir de laquelle celui-ci cesse de se subdiviser de façon fractale, est liée à la taille du libre parcours
moyen de la molécule d’oxygène à température du corps.
La dimension utilisée est celle de Hausdorff, et on observe qu’elle
correspond à une caractéristique nouvelle des surfaces irrégulières.
On connait les plages de validité des dimensions de Hausdorff observées sur
Terre pour les montagnes, les nuages, etc.
Des exemples de figures fractales sont fournis par les ensembles de
Julia, Fatou et de Mandelbrot, la fractale de Lyapunov, l’ensemble de Cantor, le tapis de Sierpinski, le triangle de Sierpinski, la courbe de Peano ou le flocon de Koch.
Les figures fractales peuvent être des fractales déterministes ou stochastiques. Elles apparaissent souvent dans l’étude des systèmes chaotiques.
Les figures fractales peuvent être réparties en trois grandes catégories :
- Les systèmes de fonctions itérées. Ceux-ci ont une règle de remplacement géométrique fixe (l’ensemble de Cantor, le tapis de Sierpinski, le triangle de Sierpinski, la courbe de Peano, le flocon de Koch) ;
- Les fractales définies par une relation de récurrence en chaque point dans un espace (tel que le plan complexe). Des exemples de ce type sont les ensembles de Mandelbrot et la fractale de Lyapunov ;
- Les fractales aléatoires, générées par des processus stochastiques et non déterministes, par exemple les paysages fractals.
De toutes ces figures fractales, seules celles construites par des
systèmes de fonctions itérées affichent habituellement la propriété
d’autosimilitude, signifiant que leur complexité est invariante par
changement d’échelle.
Les fractales aléatoires sont les plus utilisées dans la pratique, et
peuvent servir à décrire de nombreux objets extrêmement irréguliers du
monde réel. Les exemples incluent des nuages, les montagnes, les turbulences de liquide, les lignes des côtes et les arbres. Les techniques fractales ont aussi été utilisées dans la compression fractale d’images, de même que dans beaucoup de disciplines scientifiques.
Dimension fractale :

Ensemble de Julia
La dimension d’une ligne droite, d’un cercle et d’une courbe régulière est de 1.
Une fois fixés une origine et un sens, chaque point de la courbe peut être déterminé par un nombre, qui définit la distance entre l’origine et le point. Le nombre est pris négativement s’il faut se déplacer dans le sens opposé à celui choisi au départ.
La dimension d’une figure simple dans le plan est de 2. Une fois un repère défini, chaque point de la figure peut être déterminé par deux nombres. La dimension d’un corps simple dans l’espace est de 3.
Une figure telle qu’une fractale n’est pas simple. Sa dimension n’est plus aussi facile à définir et n’est plus forcément entière. La dimension fractale, plus complexe, s’exprime à l’aide de la dimension de Hausdorff.
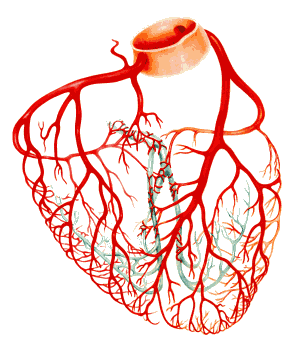
Des formes fractales approximatives sont facilement observables dans la nature.Ces objets ont une structure autosimilaire sur une échelle étendue, mais finie :
les nuages, les flocons de neige, les montagnes, les réseaux de rivières, le chou-fleur ou le brocoli, et les vaisseaux sanguins.
Les arbres et les fougères sont de nature fractale et peuvent être modélisés par ordinateur à l’aide d’algorithme récursif comme les L-Systems.
La nature récursive est évidente dans ces exemples ; la branche d’un
arbre ou la fronde d’une fougère sont des répliques miniatures de
l’ensemble : pas identiques, mais de nature similaire.
 Le chou romanesco
Le chou romanesco
Une fougère fractale modélisée en utilisant un système de fonctions itérées.
La surface d’une montagne peut être modélisée sur ordinateur
en utilisant une fractale :
prenons un triangle dans un espace tridimensionnel dont nous connectons les milieux de chaque côté par des
segments, il en résulte quatre triangles.
Les points centraux sont
ensuite déplacés aléatoirement vers le haut ou le bas, dans un rayon
défini.
La procédure est répétée, diminuant le rayon de moitié à chaque
itération. La nature récursive de l’algorithme garantit que le tout est statistiquement similaire à chaque détail.
Enfin, certains astrophysiciens ont remarqué des similitudes dans la répartition de la matière dans l’Univers
à six échelles différentes. Les effondrements successifs de nuages
interstellaires, dus à la gravité, seraient à l’origine de cette
structure (partiellement) fractale.
Ce point de vue a donné naissance au
modèle de l’univers fractal, décrivant un univers fondé sur les fractales.
Les domaines d’application des fractales sont très nombreux, on peut citer en particulier :
- en biologie, répartition des structures des plantes, bactéries, feuilles, branches d’arbres…
- en géologie, étude du relief, côtes et cours d’eau, structures de roches, avalanches…
- en paléontologie, loi de puissance des apparitions et extinctions d’espèces
- en morphologie animale, structures des invertébrés, plumes d’oiseaux…
- en médecine, structure des poumons, intestins, battements du cœur
- en météorologie, nuages, vortex, banquise, vagues scélérates, turbulences, structure de la foudre
- en volcanologie, prévision d’éruptions volcaniques, tremblements de terre
- en astronomie avec la description des structures de l’univers, cratères sur la Lune, répartition des exoplanètes et des galaxies…
- en sciences humaines, structure urbaine, évolution de la démographie
- en économie et finance, prévision des krachs boursiers (théorie des fractales)
- en électronique, antennes larges bandes des téléphones portables
- dans les arts, art graphiques bien sur, mais aussi en littérature, en musique, au cinéma…
Utilisation des Fractales dans la vie courante :
Tous ces domaines – et bien d’autres – peuvent bénéficier de la description et d’une modélisation en termes fractals des phénomènes associés.
Le modèle commence tout particulièrement à se développer en finance, où l’approche fractale de Mandelbrot se prête aux marchés volatils.
La société de gestion d’actifs Bryan Garnier Asset Management utilise ainsi dans la gestion de son fonds Bryan Garnier Opportunités un modèle identifiant les répétitions mathématiques afin de prévoir certains mouvements de prix à court-terme.
Cette approche systematique est basée sur la volatilité et l’accélération des échanges de titres afin de valider les tendances. Une anticipation des variations est ainsi immédiatement inscrite sur le modèle: si la variation est d’ampleur suffisante, elle permet de prendre par exemple une position short sur le marché.
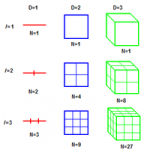
Le Fractale et ses Dimensions :
En géométrie fractale, la dimension fractale, D, est une grandeur qui a vocation à traduire la façon qu’a un ensemble fractal de remplir l’espace, à toutes les échelles. Dans le cas des fractales, elle est non entière et supérieure à la dimension topologique.
Ce terme est un terme générique qui recouvre plusieurs définitions. Chacune peut donner des résultats différents selon l’ensemble considéré, il est donc essentiel de mentionner la définition utilisée lorsqu’on valorise la dimension fractale d’un ensemble.
Les définitions les plus importantes sont
la dimension de Hausdorff-Besicovitch, la dimension de Minkowski (ou « box-countig »), et la dimension de corrélation.
 Dans le cas d’ensembles fractals simples (auto-similarité stricte, notamment) on conjecture que ces définitions donnent des résultats identiques.
Dans le cas d’ensembles fractals simples (auto-similarité stricte, notamment) on conjecture que ces définitions donnent des résultats identiques.
Par abus de langage, on trouve parfois le terme « dimension fractale » pour désigner des grandeurs non géométriques telles que l’exposant de lois de puissance dans des lois de distribution statistiques ou des séries temporelles, invariantes d’échelle, notamment en finance.
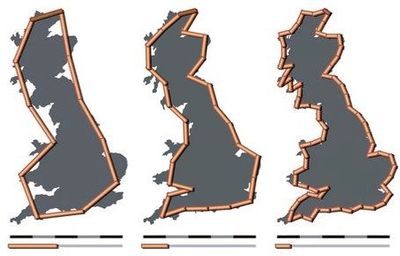 La mesure de la dimension fractale trouve des applications dans de nombreux domaines de recherche tels que la physique, l’analyse d’image, l’acoustique l’analyse des zéros de la fonction de Riemann ou les processus electrochimiques.
La mesure de la dimension fractale trouve des applications dans de nombreux domaines de recherche tels que la physique, l’analyse d’image, l’acoustique l’analyse des zéros de la fonction de Riemann ou les processus electrochimiques.
L’estimation de la dimension fractale d’objets réels est très sensible au bruit et à la quantité de données disponible.
On doit donc être prudent concernant la valeur obtenue.
Les définitions de dimension fractale présentées dans la sections précédentes s’entendent à la limite, lorsque E tend vers zéro. Or cette limite n’est jamais atteinte dans le monde physique à cause des limites moléculaire ou quantique. Pour cette raison il n’existe pas d’objet physique fractal au sens strict.
La dimension fractale n’est, en pratique, calculée que sur un intervalle défini, généralement pour des valeurs de E visibles (ou significatives vis-à-vis des propriétés que l’on souhaite étudier). On définira ainsi une dimension fractale apparente ou approximative.
La mesure d’une telle dimension fractale apparente utilise souvent la méthode de Minkowski-Bouligand ou méthode « box-counting » par comptage de boîtes.
Cette restriction peut également concerner des constructions purement géométriques. À titre de contre-exemple, dans l’illustration ci-contre, on a défini une figure fractale paradoxale ayant l’aspect de la courbe de Koch mais ayant la dimension fractale de L’ensemble de Cantor ( voir lien )
Fractales – A la recherche de la dimension cachée ( 50mn )
Partager ce savoir à vos proches en cliquant sur le bouton ci-dessous.
Paix et sincérité à tous.
Eveil-delaconscience











Vous devez vous connecter pour laisser un commentaire.